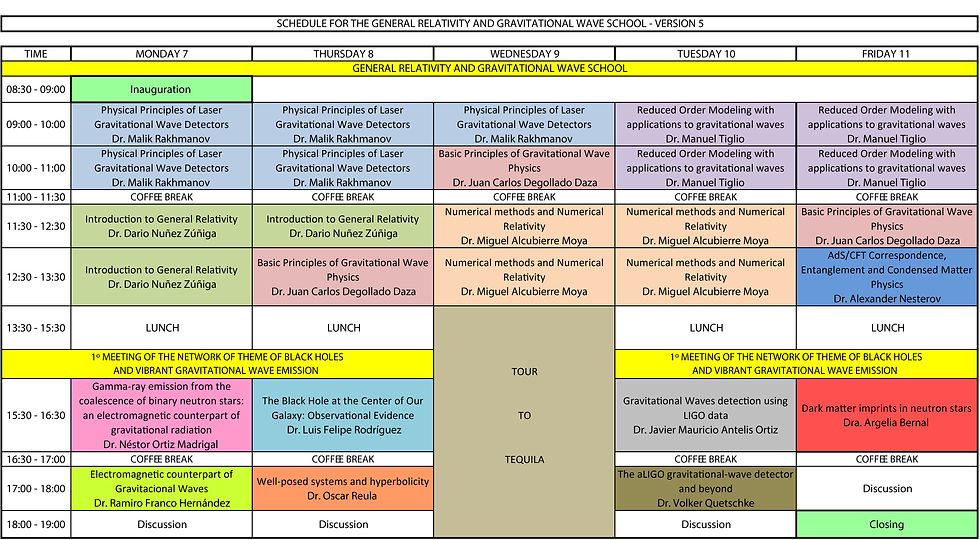
SCHEDULE

The program is divided into two sections, in the morning will be held the School of General Relativity aimed at undergraduate and graduate levels. In the afternoon we specialized talks to which can assist both students and teachers.

Course content

Numerical methods and Numerical Relativity

Dr. Miguel Alcubierre

1) The formalism 3 +1
2) Hyperbolic Systems
3) Approximations finite difference
4) Simple applications of numerical relativity

Introduction to General Relativity

Dr. Darío Núñez

1) Basic concepts of special relativity
2) Basic concepts of tensor algebra
3) Basic concepts of differential geometry
4) Essential Proposal and derivation of Einstein equations
5) Properties of the solution corresponding to a black hole
6) Properties of cosmological solution

Basic Principles of Gravitational Wave Physics(2h + 1h de Mathematica)

Dr. Juan Carlos Degollado

1) General Relativity linearized
2) Monochromatic Gravitational waves
3) Description in the Transverse system without trace
4) Energy and momentum of gravitational waves
5) Generation of gravitational waves
6) Binary systems

Physical Principles of Laser Gravitational Wave Detectors

Dr. Malik Rakhmanov

1) Gravitational waves in the coordinate frame of the detector (local Lorentz gauge)

2) Inertial test masses for sensing gravitational wave (displacement measurement)

3) Photons in the field of the gravitational wave (photon round trips)

4) Fabry-Perot resonator as GW detector

5) Pound-Drever-Hall locking scheme (optical heterodyne method)

6) Michelson interferometer with Fabry-Perot Arm cavities

7) The concepts of power and signal recycling in GW interferometers

8) Angular sensitivity of laser interferometric GW detectors (antenna patterns)

9) Detection of GW with the network interferometers (maximum likelihood method)

10) Rank deficiency and regularization techniques for signal extraction

Reduced Order Modeling with applications to gravitational waves

Dr. Manuel Tiglio

In these lectures I will present a high level overview of Reduced Basis (RB) for parameterized systems. This is the predominant approach for reduced order modeling, both for forward (simulations) and inverse (inference) problems and is based on an offline-online decomposition. In the offline stage one builds a reduced model to represent the truth one. If there are regularity conditions on parameter variation, the reduced model converges very fast with the number of bases, in most cases of interest to gravity, exponentially (as opposed to sub-linear in Montecarlo simulations). This involves approximation theory and it will be described why and how RB with a greedy approach is nearly optimal with respect to an optimal representation (the Kolmogorov n-width, an NP complex problem). The RB-greedy approach is of linear complexity and, among many advantages, embarrassingly parallel and hierarchical. Next, an agnostic, data-driven approach will be presented for a predictive, or surrogate model, which can be exactly equivalent (up to machine precision) to the truth one but with significan speedups. In binary black hole simulations this has shown a speedup factor of 11 orders of magnitude while being indistinguishable from supercomputer simulations, with the difference that it can run on a millisecond on a laptop or even on a smartphone (an app will be presented and distributed). Parameter estimation has been reduced from months/years of wall time computational time to hours, without loss of accuracy. While most literature on the topic focus on “certified” approaches for linear elliptic partial differential equations, the focus here will be on agnostic or data-driven ones, with the above demonstrated speedups, which can be applied to a large number of disciplines, from finances to biology and more.
An industrial-grade open source software on the works will be introduced.
A pressing need and current topic of cutting-edge research is to include stochastic components through generalized Polynomial Chaos (gPC) and merge it with RB. Another promising area that will be sketched is the combination of RB with manifold learning.
Basic knowledge at the undergraduate level is required to follow these lectures.

Some references:

- An overview of RB in an agnostic way:

http://journals.aps.org/prx/abstract/10.1103/PhysRevX.4.031006 (free to access)

- 11 orders of magnitude speedup of lossless binary black hole simulations:

http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.121102

http://arxiv.org/pdf/1502.07758.pdf

- Up to 130x lossless speed-up in LIGO parameter estimation:

http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.114.071104

http://arxiv.org/pdf/1404.6284.pdf

- Connection to manifold learning:

http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.113.021101

http://arxiv.org/pdf/1401.7038.pdf